| CLICK HERE FOR INDEX PAGE | |
| THE BINARY NUMBER SYSTEM | |
| V. Ryan © 2004 - 2009 | |
|
PDF FILE - CLICK HERE FOR PRINTABLE VERSION OF WORK SEEN BELOW |
|
|
|
|
|
Binary numbers are closely related to digital electronics. With digital
electronics a ‘1’ means that current
/ electricity is present and a ‘0’
means it is not present. The different parts of a computer communicate
through pulses of current (1s and
0s). |
|
|
|
|
|
|
|
|
|
|
|
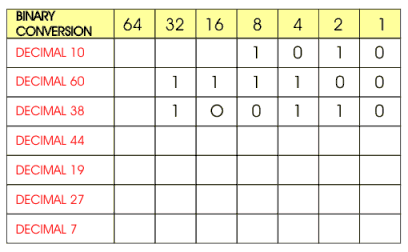
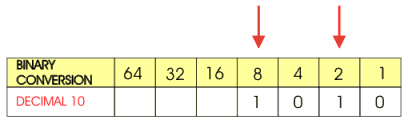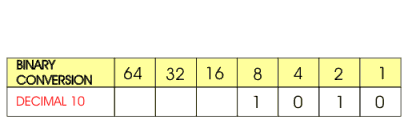
Look at the row that represents the decimal number 10 (diagram below). The table can be used to convert this decimal number to a binary number. The table shows that DECIMAL 10 is composed of one number 8 and one number 2. Zeros are used to fill the blank spaces which gives 1010 as the binary equivalent of decimal 10. |
|
|
|
|
|
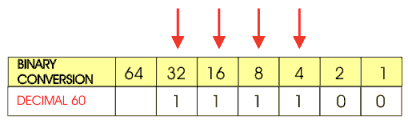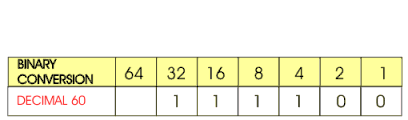
Next look at the way decimal 60 is converted to its binary equivalent. 60 is composed of one 32, one 16, one 8, and one 4. The blanks are filled with zeros giving 111100 as the binary equivalent of decimal 60. |
|
|
|
|
|
The important point to remember is that when converting from decimal to binary OR from binary to decimal, you must write down the top section of the table (seen in yellow above) and underneath enter the binary number. |
|
|
QUESTIONS: |
|
|
|
|